All About Gain

INTRO: For those interested in headphone amps, gain is an important topic. Here are the essentials about gain with lots of links to more information. In addition to this introduction explaining gain, there are later sections on:

• Excess Gain
• Gain Calculations
• Gain Details

RELATED ARTICLES: The following may be useful understanding how gain fits into the bigger picture:

• Headphone Amps Explained
• Amplifier Power Requirements
• Noise And Dynamic Range

WHAT IS GAIN? Put simply, gain is the maximum amount an amplifier can increase a signal. In the world of headphones, it's usually voltage gain. The diagram above shows a source with a weak output made 3 times stronger by an amplifier. Applying gain to a signal doesn’t normally change the dynamic range, it just makes everything louder. Other ways to specify gain, such as power and current, are rarely used for headphone gear.

YACA (Yet Another Car Analogy): The relationship between gain, volume, and maximum power can be confusing to some. Using car analogies might help:

• Gain Is Like The Gear Selection - When a car is in its lowest gear its top speed is limited to a fairly low value but it can climb steep hills. It's somewhat the same with a headphone amp set to low gain. Think of a gain switch as 1st, 2nd, and 3rd gear on a car's transmission. Different gears are used for different driving conditions.
• Volume is like the Throttle (Accelerator) - The volume control adjusts the overall power to the headphones much like the throttle in a car adjusts the power to the wheels.
• Maximum Power is like Top Speed - Most cars are capable of going faster than most people need. While a car might have a top speed of 100 MPH, in first gear, it might only do 40 MPH. So gain can be used as a way to limit maximum output and better match the output to a given pair of headphones. The difference between the top speed and the highest speed limit is somewhat analogous to excess gain.

WHY DOES GAIN MATTER? If you don't have enough gain, your headphones probably won’t get loud enough. If you have too much gain, you will be forced to use only a small portion of the volume control's range, there may be increased channel balance problems, more noise, more distortion, and you could even damage your headphones more easily. Most any amp will perform worse at higher gain settings so you want to use the least amount of gain that gets the job done.

GAIN AND VOLUME ARE IMPLEMENTED DIFFERENTLY: Turning down the volume is not the same as lowering the maximum gain (with a few rare exceptions). A race car doesn't turn into a family car if you never use more than half throttle. Certain compromises were made in the race car that make it less suitable for family car duty even if you try to drive it slowly. The same is true with a high gain amp. It's important to not have much more gain than you really need.

GAIN CAN BE USED TO LIMIT MAXIMUM POWER: If you have some fairly efficient headphones that are as loud as you would ever want with only 0.7 volts of audio. But you have a high-end desktop headphone amp that can put out 10 times as much (7 volts). By reducing the gain, even if you accidentally turn the volume all the way up, you can limit the maximum power to your headphones. This can help prevent hearing damage and even headphone damage. It also also allows using much more of the volume control's range making volume adjustments easier and more accurate.

GAIN CAN CHANGE WITH DIFFERENT HEADPHONE LOADS: If an amp doesn’t have an output impedance below 2 ohms the gain will change with different loads. The higher the output impedance, the more dramatic the change. For example, an amp with a 120 ohm output impedance with 5X gain at no load, will have only 3.5X gain with 300 ohm headphones and only 0.6X gain with 16 ohm headphones. This is another reason it’s important to know the output impedance.

GAIN CANNOT CORRECT FOR A LACK OF MAXIMUM POWER: If your headphones need 5 volts but your amp is only good for 2 volts cranking up the gain won't help any and will just make the amp clip sooner. Clipping is what happens when an amp runs out of power. The rest of this article assumes your amp is capable of enough power for your headphones. For more on this topic see: More Power?

 

---

GAIN DETAILS

---

HOW IS GAIN EXPRESSED? Gain is usually expressed as a factor (ratio), such as 4X, or in decibels (dB) such as 12 dB. In this case, 4X is the same as 12 dB and simply means with the volume control set to maximum, the output voltage of the amplifier will be four times higher than the input voltage. If you put 1 volt in you will get 4 volts out (assuming you don't exceed the maximum output capability). I show how to convert from ratios to dB and back in the Gain Calculations section below.

WHAT ARE TYPICAL GAINS? Headphone amps that have just a single fixed gain typically range from 2X (6 dB) to 5X (14 dB). For amps with two gain settings, low gain might be 2X to 3X and high gain 5X to 8X. Some amps have three or more gain options while others allow changing internal jumpers or resistors to set the gain.

A ROUGH GUIDELINE: If you want to skip the more technical details, the table below offers some idea of what gain will be usable with various headphones and sources:

Headphones	Portable	USB DAC	HOME	< Source
IEM 100 - 115 dB/mW 16 - 32 ohms	1X/0 dB	1X/0 dB	1X/0 dB
Sensitive Low Impedance Full Size Grado, Denon, Etc.	2X/6 dB	1X/0 dB	1X/0 dB
Average Full Size HD5xx/600/650 100 - 300 ohm	5X/14 dB	3X/10 dB	2X/6 dB
High Impedance Full size 300 - 600 ohm	10X/20 dB	5X/14 dB	3X/10 dB

DO I NEED AN AMP AT ALL? If your headphones already get plenty loud enough, and you're happy with the sound, odds are you don't need an amp. But if they don't get loud enough, an amp may be required. The table above shows several combinations where the gain is listed as 1X which implies no amp is required. But you might still want to use an amp to lower the output impedance of your source. For example, the iPod Touch 3G has a 7 ohm output impedance. With balanced armature IEM headphones this causes audible problems. See: Output Impedance. So while the IEMs don't need any more voltage they can still benefit from a lower output impedance. Some amps, like the O2, can be easily configured for 1X gain and improve the sound of higher impedance sources. For more on headphone amps in general, see: Headphone Amps Explained

 

---

EXCESS GAIN

---

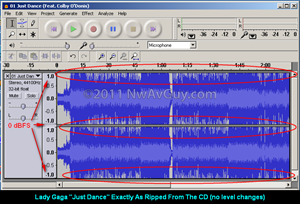
EXCESS GAIN: If your amp has just enough gain for your headphones to hit the desired level at full volume with a 0 dBFS signal it's sort of like having a car with a top speed equal to the highest speed limit in your area. There might be times when you want to go even faster. But how much extra do you need? The amount of volume control range above where a 0 dBFS signal clips is considered “excess gain”. Here are some points to consider:

• Excess Gain Is A Tradeoff - As described above in Why Does Gain Matter, too much gain has negative side effects. So it's a tradeoff between those side effects and how much excess gain you want.
• Excess Gain Is Only Useful For Quiet Tracks - Most properly recorded digital music is designed to hit, or get within 1 dB of, 0 dBFS. If your amp has excess gain, using full volume with normal tracks will cause the amp to clip (badly distort) and may even damage your headphones. But, without excess gain, rare quiet tracks may not be loud enough even with the volume at 100%. One solution is having a reasonable amount of excess gain. Another solution is to normalize quiet tracks to 0 dBFS using Audacity or other software. This simply raises the levels so the loudest portion of the track is at 0 dBFS. Yet another solution is to use ReplayGain which helps equalize all tracks to roughly the same perceived volume. 
• ReplayGain (volume leveling) - If you use something like ReplayGain nearly all of your music should play at a consistent subjective level. ReplayGain is essentially like having someone automatically adjust the volume for each track (or CD). The default target loudness of 89 dB leaves 14 dB of headroom between the average volume and 0 dBFS. For the most compressed pop music this means the peak levels will be as much as 6 dB below 0 dBFS, while dynamic music will get much closer to, or even hit, 0 dBFS. If you use ReplayGain, or something similar, for volume leveling, you may want up to 6 dB of excess gain to allow for the overall volume reduction ReplayGain applies to some tracks. For more on average volume see: More Power?
• Dynamic Range – It’s important to note that neither the gain of an amplifier, nor ReplayGain, normally changes the dynamic range of music. Gain changes normally apply equally to the softest and loudest portions of the signal (music). To change the dynamic range you have to apply compression, limiting, (or dynamic range expansion).
• Clipping vs Maximum SPL – Some amps have plenty of power and your headphones, or ears, will give up before the amp does when dialing up excess gain on a recording that already hits 0 dBFS. But, in some circumstances (especially with low sensitivity headphones), the amp might run out of power first. If you want to be assured your amp will never clip, just work backwards from the amp’s maximum output into your headphone impedance to determine the gain. If your amp maxes out at 7 volts, and your source is 2 volts, set the gain to 3.5X and the amp will never clip even at full volume with a worst case recording.  See: More Power?
• 9 dB Excess Gain Is A Reasonable Maximum - I would aim for at least 3 dB of extra gain but somewhere around 9 dB the negative side effects already mentioned start to outweigh the advantages. A few might want to go as high as 12 dB but only if they've used something like ReplayGain to normalize their music library to a lower than normal average volume or have other unusual requirements.
• The Math – 3 dB of extra gain means multiplying the minimum gain by 1.4 and for 6 dB multiply by 2, and for 9 dB multiply by 2.8.

THE CHANNEL BALANCE PROBLEM: Devices with conventional volume controls may have audible channel imbalance at very low volumes. It's extremely difficult to manufacture volume control potentiometers that maintain tight channel balance below about -40 dB (referenced to full volume). Having too much excess gain forces using only the lower portion of the volume control's range with normal recordings. If your amp has 10 dB of excess gain, for example, -40 dB below 0 dBFS on the volume control is -50 dB below full volume. The channel balance error will likely be much greater and more audible. Some products get around this problem by using digitally controlled electronic volume controls that can maintain better channel balance at low settings but these can add distortion and often controlled by up/down buttons rather than a simple knob. Stepped precision attenuators are another solution but are expensive and sometimes their step size is too great.

 

---

GAIN CALCULATIONS

---

HOW DO YOU CONVERT FROM Gain Ratio X TO dB? The math requires using a function known as base 10 logarithm (LOG on a calculator). But you can also just use an online dB calculator:

• Online dB Calculator
• Gain in dB = 20 * LOG₁₀ ( Gain Factor ) [i.e. 20 * LOG₁₀ ( 4 ) = 12 dB]
• Gain Factor = ANTILOG₁₀ ( Gain in dB / 20 ) [i.e. ANTILOG₁₀ ( 12 / 20 ) = 4X]

HOW MUCH GAIN DO I NEED? This comes down to only three things:

• How much voltage your headphones need
• How much output your source has
• How much excess gain you want.

HEADPHONE REQUIREMENTS: For a given pair of headphones, the More Power? article helps determine what your headphones need. This is related to the sensitivity and impedance of your headphones which vary widely. The most efficient IEMs only need about 0.1 volts to play loudly, Sennheiser HD600s need about 2.3 volts and Beyer DT880-600s need about 6 volts or 60 times more than the IEMs.

SOURCE OUTPUT LEVEL: Sources have a maximum output level. It's the output voltage at 0 dBFS (the loudest digital music can get) and at full volume (if the source has a volume control). Sources can be roughly divided into the follow categories (all voltages are Vrms):

• Portable Players - Most of these have a maximum output of 0.5 - 1.0 volts from either their headphone jacks or LOD (Line Output Dock) connectors. The iPod Touch is 0.5 volts from the LOD.
• USB Powered DACs - Most of these have a maximum output of 1.5 volts or less.
• Normal Home Audio Gear - The Redbook standard for any home equipment that plays digital audio is 2 volts. Some go slightly higher up to 2.5 volts. There are also a few USB powered DACs that can manage similar voltages (such as the HRT Music Streamer II).
• Unusual (rare) Home Sources - A few companies, arguably unwisely, have decided to go well above the established standard and output more than 2.5 volts. But I'm not aware of any that go above 3.3 volts unless they have a volume control.
• Balanced Outputs - These can be misleading because balanced outputs normally have twice the output of unbalanced outputs. A 4 volt balanced output, used with an unbalanced adapter or cable, is really only 2 volts.
• Unknown Sources – See DIY Gain Measurements below.

CALCULATING THE REQUIRED GAIN: Once you've figured out the above three requirements, it's fairly easy to calculate the gain you need. Just follow these steps (examples are given for the HD600's driven from an iPod LOD with 3 dB excess gain):

• Calculate Minimum Gain: Gain Factor = Vout / Vin [i.e. 2.3Vout with 0.5V Vin = 2.3/0.5 = 4.6X]
• Convert To dB: Minimum Gain in dB = 20*LOG( Gain Factor ) [i.e. 20*LOG(4.6) = 13.2 dB]
• Add Excess Gain: Final Gain in dB = Minimum Gain + Excess Gain [i.e. 13.2 + 3 = 16.2 dB]
• The result is 16.2 dB (6.5X) of gain for the example case.
• You can also multiply 4.6X by 1.4 to get 6.5X (1.4 is 3 dB excess gain as a ratio)
• If you know the output impedance multiply by (Zload + Zout) / Zload

INPUT OVERLOAD: Also be aware that many devices, especially portable ones, have inputs that can be overloaded by certain sources. Because the Redbook standard is 2 volts, a lot of devices are designed to only handle about 2.1 volts such as the FiiO E9 desktop amp. And the portable FiiO E7 overloads at about 1.2 volts on the input because it was designed for use with portable players which are generally under 1 volt. Sometimes the input overload point may depend on the gain settings. So check the documentation for a given amp--especially if you plan to use home sources with a portable amp, or sources with more than 2 volts of output.

RESISTOR VALUES: Some amplifiers let you set the gain by changing resistor values. The diagram to the right shows a typical non-inverting amplifier stage. The gain is given by 1 + 1000/500 = 3. For all the math, see Wikipedia Gain and Wikipedia Amplifiers. Some amplifiers may have multiple gain stages, in which case you have to multiply the gain of each stage together. So an amp with a 2X and 3X stage has a total gain of 6X.

DIY GAIN MEASUREMENTS: If you have a decent DMM (multimeter) that can measure x.xx volts AC (i.e. 0.01 volt resolution) you can play back a 60hz 0 dBFS sine wave and measure the output of your source in Vrms. You can create the file with Audacity. Ideally the voltage should be measured using a “Y” cable with your source connected to the amplifier. You can then also (carefully so not to cause short circuits) measure the output of your amplifier. Don’t connect your headphone as they could be damaged. And don’t try higher frequencies as most meters are not accurate much above 60 hz. Vout/Vin = Gain

BOTTOM LINE: Gain is important. There's a definite sweet spot for most headphones and sources. The closer an amp comes to having the ideal gain, the better overall performance you will get.

Noise & Dynamic Range

INTRO: Noise is generally more obvious with headphones than speakers and a relatively common complaint among headphone aficionados. There’s a lot of confusion about sources of noise, specifications, and how to make valid comparisons.

NOISE DEFINED: Technically noise is anything present that’s not related to the desired audio signal. We usually only care about noise within the audible range of 20 hz to 20 Khz. And within that range, the ear is more sensitive to noise at some frequencies than others. The most common audible noise is relatively random in nature and heard as a broadband “hiss”. Low frequency hum at power line frequencies is also sometimes audible. And digital devices, especially computers and mobile phones, can generate noises at specific frequencies that are heard as whines, chirps, clicks, buzzes, etc.

SOURCES OF NOISE: Noise can, and often does, invade the signal chain in audible ways starting at the microphones used during recording. Here are some common sources:

• Recordings – Microphone preamps and other gear used during recording often have audible noise. But lots of techniques are used to reduce the audibility of such noise. Noise gating, for example, is used to cut noise when there’s no sound from a given microphone or instrument. Nearly all recordings before the early 80’s were mastered on analog tape which has significant amounts of tape hiss. And even digital recordings can have noise from all the electronics in the signal path. And, of course, vinyl has lots of noise.
• DAC – In theory a perfect 16 bit DAC has a 96 dB signal-to-noise ratio but some fall well short of full 16 bit performance. 24 bit DACs often only manage approximately 16 bit performance and the very best reach 21 bit (ENOB) performance. This is especially true of DACs inside a computer. Some DACs also produce significant amounts of their own noise such as as modulation and quantization noise (although these can also be considered forms of distortion as they are only present with a signal).
• Headphone Amp – Even a laptop or portable player has a headphone amp in it although it might be built into the same chip as the DAC. Any amplifier adds noise, it’s just a question of if it’s audible or not. Even some fairly expensive stand-alone headphone amps can have significant amounts of noise. They can also further amplify whatever noise is “upstream”.
• Noise is Cumulative – While sometimes there’s an obviously dominant source of noise it can just as easily be a little from here and little from there. Noise adds up.

NOISE MEASUREMENTS: There are two basic kinds of noise measurements. One is a an absolute measurement of just the noise and the other is a measurement of the noise relative to some known signal level. The decibel (dB) was partly developed as it more closely follows subjective human hearing. A one dB change in level is about the smallest change most people can detect. A 10 dB change is perceived as being roughly twice as loud (or soft). If Gear A has noise of -80 dBv and Gear B is -70 dBv the second one will have about twice the subjective noise:

• Absolute Noise – This is normally measured in microvolts and is the total output with no signal present. It indicates the noise “floor” which is useful from an analytical point of view but less useful for subjective noise evaluation where you’re more concerned about the noise compared to a given realistic listening level. All noise downstream of the volume control is absolute noise.
• Relative Noise – This is a more useful measurements as it correlates the noise relative to some known amount of signal. There are decibel units that are referenced to known standards. The most common are dBv and dBu. Noise given in dBv is referenced to a signal of 1 volt RMS and dBu is referenced to 0.775 volts. Both are reasonable listening levels for many full size headphones such as the Sennheiser HD600.
• Signal to Noise Ratio (SNR or S/N) – This is a more open ended method where both the noise figure and the reference signal level must be provided for it to be a meaningful number. The correct unit is dBr where the “r” means “relative” but it’s often just given in dB. Unfortunately, many manufactures don’t specify the reference level. When just SNR is specified with no reference you should assume it’s referenced to whatever the absolute maximum output level is for the device--the same as a Dynamic Range measurement. Sadly, that’s often not specified either (see: More Power).
• Volts vs dBv vs dBu vs dBr – Measuring noise in volts only works for absolute noise measurements. Measurements in dBv are referenced to 1 volt which makes the math much easier and they’re commonly used in professional audio. 0 dBv = 1 volt. In consumer equipment dBu is more common and referenced to 0.775 volts making the math more awkward. Measurements in dBr can be referenced to anything including each other.

DYNAMIC RANGE: As explained above, Dynamic Range is really the same as the Signal-to-Noise Ratio (SNR) using the maximum possible signal. It’s the ratio between the loudest undistorted output of the device and what’s left over when nothing is playing and is usually a positive number instead of a negative one. The theoretical dynamic range of 16 bit digital audio is 96 dB so that’s often used a benchmark for dynamic range—ideally you don’t want the playback hardware to be worse than the recording format. With higher output gear it’s not uncommon to see dynamic range measurements well above that value so it’s not an unrealistic target. Studies, such as the one conducted by Meyer and Moran, have shown 96+ dB of dynamic range is transparent for any normal listening conditions. The only way to expose the noise floor is to crank up the volume to unrealistic levels. Using a digital (software) volume ahead of a 16 bit DAC and leaving the volume after the DAC cranked way up may expose the 16 bit noise floor. In these applications 110 dB of dynamic range should be sufficient to keep the noise below ambient levels.

VOLUME SETTING: There are some interesting twists with volume settings some of which are not intuitive:

• Upstream Noise - Any noise that’s “upstream” of the volume control will be more audible as you turn the volume up assuming the music doesn’t mask it. The absolute noise is worse at higher volume settings but the SNR stays about the same because you’re also increasing the signal by the same amount as you turn up the volume.
• Amplifier Noise – Depending on where the volume control is located within the gear it may or may not significantly alter the noise. A digital volume control, for example, will only affect the noise in the recording itself (and not change SNR at all). Interestingly some devices with analog volume controls have the most noise at half volume—such as the FiiO E9. This is usually because you’re hearing the Johnson Noise of the volume control itself where half volume is the worst case situation. This is typical when the volume control is before the gain stage. When the volume is after the gain stage, most everything becomes Upstream Noise (see above) and is reduced at lower volume settings.
• Fixed Noise – Amps have a certain amount of noise that’s present at any volume setting. This is usually noise that’s from the circuitry after the volume control and, in a properly designed amp, it’s entirely possible to have it always be inaudible.

WORST CASE NOISE AUDIBILITY: Some define audible noise as anything you can hear under worst case conditions—i.e. nothing playing, the worst case volume and gain settings, a very quiet room, and using extremely sensitive headphones. An easily accepted guideline is –96 dB un-weighted referenced to a realistic maximum listening level (see Dynamic Range above) as that’s the maximum dynamic range of 16 bit digital audio. So whatever level produces around 110 dB peak SPL (see my Power article) should be the reference value and as long as the noise is about 96 dB below that it will be entirely inaudible. That’s achievable with less sensitive headphones but difficult with ultra sensitive IEMs. Some examples

• HD600 – 2.3 V for 110 dB gives 36 uV or –88 dBv of noise
• GRADO SR80 – 0.7 V for 110 dB gives 11 uV or –99 dBv of noise
• U.E. TripleFi 10 – 0.1 V for 110 dB gives 1.6 uV or –116 dBv of noise

PRACTICAL NOISE AUDIBILITY:  In reality, testing shows that 85 dB below 110 dB SPL is sufficiently quiet for most people (noise of 25 dB SPL). That puts the limit at –105 dBv, (-102.8 dBu) or 5.6 uV for sensitive IEMs. With the most sensitive IEMs in a really quiet room someone might still hear some noise at that level, but being realistic, it’s likely “good enough”. If you want to be assured of silence with even the most sensitive IEMs, aim for –110 dBv (-107.8 dBu).

NOISE & GAIN: Headphone amps have varying amounts of gain--the maximum amount they can amplify the input signal. Some have multiple gain settings. The higher the gain the more they will amplify upstream noise. And, typically, the higher the gain the higher their own noise. This is one reason you ideally want to use the lowest amount of gain required. See: All About Gain

AN EXAMPLE: The O2 Headphone Amp has the following measurements (see O2 Measurements):

• Noise dBv Volume 100% – The O2 measures –112 dBv un-weighted and –115 dBv A-Weighted. This is well below the –105 dBv guideline and means the O2 will be silent in use.
• SNR Referenced to Full Output – The O2 referenced to 7 volt RMS (full output) measures –130 dBr unweighted and –133 dBr A-Weighted. These numbers are extremely impressive but also unrealistic for most users who will never need even close to 7 Vrms of output.

HEADPHONE SENSITIVITY: Headphones vary widely in their sensitivity. Many assume a headphone that’s 10 dB more sensitive will make the SNR 10 dB worse but that’s often not true. As headphones become more sensitive, you need less gain, and/or use lower volume settings. Both of those typically lower noise So the ratio of the signal to the upstream noise, and hence the SNR, stays about the same. Only fixed noise (see above) is directly related to the headphone sensitivity. Johnson Noise from the volume control can complicate this a bit but as headphones become more sensitive the fixed noise becomes much more important. See Noise Audibility Worst Case above for examples of three different headphones.

NOISE SPECTRUMS: Sometimes you will see a spectrum graph for noise measurements. The approximate “noise floor” in these graphs is much lower than the actual noise specification. In the graph to the right the overall noise is about –112 dBv but the noise floor is down around –150 dBv in the graph. This huge difference is because the –112 dB number is the sum of all the noise from 20hz to 20 Khz. Think of spreading a cup of sugar out across the floor. It would barely change the height of the floor. But if you gather all the sugar up in a measuring cup, you can know how much total sugar there is—much like the noise measurements shown in the boxes in the graph. Click the graph for a larger version.

NOISE BANDWIDTH AND WEIGHTING: Typically noise is the sum of all energy within the audio band. Ideally the bandwidth is specified for un-weighted measurements. A-Weighting is often used which adjusts the measurement for the relative sensitivity of the ear at different frequencies and also limits the bandwidth. Another weighting standard is ITU-R 468. For gear that’s prone to a lot of out-of-band ultrasonic noise, such as Class-D amplifiers and digital equipment, a wideband noise measurement up to about 100 Khz can also sometimes be useful in addition to weighted/limited measurements.

COMPARING NOISE MEASUREMENTS: You can only directly compare noise measurements given in dBu, dBv, or dBr at the same reference level. And they must use a similar bandwidth and all be either unweighted or weighted the same way. Otherwise, you can’t compare the numbers without at least doing some math and sometimes you can’t compare them at all. Here are some examples:

• RMAA – Unfortunately RMAA has no concept of absolute levels. So it can’t calculate noise levels referenced to any known value. It attempts to calculate dynamic range against ) dBFS (the clipping level of the DAC itself) but even that is subject to wide variations in the device settings (i.e. volume, “record” level, etc.), calibration settings, etc. Basically RMAA noise measurements are nearly worthless and the noise of the PC sound hardware might be worse than whatever you’re trying to measure anyway. Some RMAA results are comparatively arbitrary and this is one of them.
• dBv to dBr – If Gear A has a noise spec of –100 dBv and Gear B is –108 dBr (ref 10 Vrms) at first glance B looks to be a significant 8 dB quieter. But A is referenced to 1 V and B 10 V. The difference is 20*Log(10/1) = 20 dB. So B is really 20 dB worse reference to 1V or only –88 dBv. See Generic Conversions below.
• dBu to dBv – These are close. To convert from dBv to dBu the noise is 2.2 dB worse. To convert the other way it’s 2.2 dB better.
• dBr (400 mV) to dBv – I updated my own noise measurements from dBr referenced to 400 mV to dBv (referenced to 1 volt). To convert the old 400 mV measurement to dBv the noise improves by 8 dB. To convert the other way, it’s worse by 8 dB.
• Generic Conversions – The generic math for the amount to add or subtract is 20 * Log( Vref1 / Vref2). The lower the reference voltage the worse the noise figure. Noise can also be referenced to power instead of voltage. In that case it’s 10 * Log ( Pref1 / Pref2 ).
  • dBv to Volts = antilog( dBv / 20 )
  • -96 dB in Volts = antilog ( –96/20 ) = 16 uV ( 0.000016 volts)
  • Volts to dBv = 20 * log ( Vnoise )
• Weighting Comparisons – It’s impossible to accurately compare different weighting or weighted vs un-weighted as it depends on the frequency distribution of the noise. An amp with a lot of hum, for example, will have a proportionately lower weighted measurement than one with only uniform hiss. In general, however, expect an A-Weighted measurement to be about 3 to 6 dB better than an un-weighted measurement.

SOURCE IMPEDANCE: Johnson Noise is often a dominant source of noise in headphone amps and preamps. And it’s proportional to the impedance of the input circuitry which includes the source. The higher the source impedance, the higher the noise. So, for example, a given headphone amp might be dead silent when driven from a source with a 100 ohm impedance, but using a source with a 10K impedance could easily produce audible noise. In this case the noise you’re hearing is really coming from the upstream source not the amp.

MEASURING NOISE: Because noise measurements are a sum of the noise across the audio band, and extremely low in value, they’re tricky to measure accurately. The best high-end 24 bit PC sound hardware may have a low enough noise floor, but often cannot accept the full output of the device being tested. And more significant, PC sound hardware has no way to set or measure absolute levels—i.e. measurements in volts, dBv, etc. Very few Digital Multi Meters (DMMs) have the resolution and low enough internal noise to measure accurately down to a few microvolts of AC from 20 hz to 20 Khz. It is, in theory, possible to temporarily calibrate a 24 bit soundcard using a known accurate meter and suitable test tones. But it’s tricky to do accurately and apply to whatever software is being used. The source impedance is also an issue. Manufactures tend to short circuit the inputs for the best noise number, a more realistic test is to use a shunt resistance equal to the output impedance of a typical source. If you try to use a real source, its noise will also be included in the measurement (as with RMAA). Also, when measuring a source with a DAC it’s necessary to use a very low level test signal as DACs shut off completely giving an unrealistic noise value if there is nothing to play. A proper audio analyzer can remove the low level signal from the measurement leaving just the noise.

RMAA MEASUREMENTS: Even if you somehow calibrate the levels, you still don’t know what RMAA is doing internally. It’s a magic “black box” with no credible documentation about how it arrives at its final numbers. What bandwidth is being used? Is the result weighted or un-weighted? Plus the unknown output noise of the  RMAA sound hardware is included in the measurement by design. Ultimately, the best way to make noise measurements is with an audio analyzer such as those from Audio Precision and Prism Sound.

BOTTOM LINE: Noise of around –105 dBv (referenced to 1 volt) will nearly always be inaudible. Noise around -95 dBv is probably “good enough” for many. Noise referenced to other values must be converted to dBv or another consistent reference before it can be fairly compared. RMAA values are nearly useless because RMAA has no concept of absolute levels. It can only provide dynamic range and it often gets even that wrong because it’s difficult to set the levels properly without proper instrumentation.

OTHER RESOURCES: These articles may also be useful:

• Headphone Amps Explained
• Amplifier Power Requirements
• All About Gain 

More Power?

INTRO: While the plugs on most headphones are compatible with the jacks on most gear that doesn’t mean the two will play nice together. Headphones vary widely in their power and drive requirements and some sources are far more capable than others. Mismatches are common. If you’re not satisfied with what you have now, or you’re shopping for new gear, this article might be worth checking out. (photo: Mikael Altemark).

THE PROBLEM: Put simply, a lot of headphones are not well suited for a lot of sources and vice-versa. There’s more involved than just using headphones with the right impedance. One of the most important things to consider is the sensitivity (efficiency) of the headphones.

THE EASY WAY (ROUGH ESTIMATE): If the sensitivity of your headphones is listed in dB/mW you can get a rough idea how much amplifier power is needed with the following table. To use the table, find your headphone’s sensitivity in the left column (use the next lowest number if it’s between two numbers). Then look at the numbers in the next 3 columns. Most should use a peak SPL of 110 dB (the middle column). But if you don’t like loud music, or listen to mostly pop music, you might be happy with 105 dB. If you like it really loud, or listen to a lot of audiophile recordings, use 115 dB.  For example, the Sennheiser HD600 is 97 dB/mW so it requires 20 mW to hit peaks of 110 dB. The tricky part is your source needs to produce at least that much power at the impedance of your headphones and some manufactures don’t do a good job specifying power output. More on that in the Tech Section. You can also use the table in reverse to look up a source’s output power and see how that might match up to different headphones.

dB/mW ↓	105	110	115	< Peak SPL
85	100.0	316.2	1000.0
88	50.1	158.5	501.2
91	25.1	79.4	251.2
94	12.6	39.8	125.9
97	6.3	20.0	63.1
100	3.2	10.0	31.6
103	1.6	5.0	15.8
106	0.8	2.5	7.9
109	0.4	1.3	4.0
112	0.2	0.6	2.0
115	0.1	0.3	1.0
118	0.1	0.2	0.5

SPECIFICATIONS DO MATTER: If you ask a lot of the audiophile manufactures why they don’t offer more complete specs for their products they often counter with something like: “specs don’t really matter”. But in this case they very much do matter. Headphones playing loudly enough with a particular source isn’t magic or something that can only be determined by trial and error. It’s entirely determined by a few numbers and some relatively simple math. It’s not like all headphone sources work well with nearly any headphones. It’s very much the opposite—compatibility problems are widespread. So the next time you hear “specs don’t matter” consider that person either mis-informed or they’re intentionally trying to mislead you.

MAXIMUM POWER vs GAIN: A headphone amp needs both enough maximum power and also enough gain to reach that power level with a given source. Sources vary widely in their output. An iPod Touch line output (LOD) only produces a maximum of 0.5 volts while most home gear has at least four times more output. So just because your amp has enough power you also need to make sure it has enough gain. See: All About Gain

POWER REQUIREMENTS vs POWER HANDLING: There’s often a big difference the amount of power headphones need to play loudly enough versus the maximum power the manufacture claims they can handle. When you see a specification that says something like “Maximum Power: 200 mW” that doesn’t mean you need, or even want, 200 mW. It only means if you use much more than 200 mW you might damage the headphones.

FIVE FACTORS: If you want know everything that goes into determining headphone and source compatibility there are five things to consider:

• Type Of Music (average volume) – Music varies widely in its average volume. Heavily compressed pop music has a much higher volume than say an audiophile jazz recording.
• Desired Maximum Output – This is simply the maximum perceived volume someone wants to listen at. It varies from person to person but it can be estimated fairly accurately several different ways.
• Headphone Sensitivity – This is how loud the headphones will play for a given power or voltage level (from the specs or professional measurements).
• Headphone Impedance – This makes a big difference in the next item and is necessary for some conversions. This is nearly always in the headphone specs.
• Source Maximum Output – This is how much power the source can produce which varies depending on the impedance of the headphones. This is often poorly specified but it is measured in proper product reviews with full measurements. You can sometimes make assumptions from what specs are provided.

AVERAGE (RMS) VOLUME: Music varies widely in average volume (also known as “RMS volume”) which roughly equates to the perceived loudness of the music. Somewhere around the early 90’s the “loudness wars” started. Recording engineers starting using more and more compression (which boosts the soft parts of music) so their mix sounded louder than other mixes. As a result, over the last two decades, the average volume of pop music has slowly risen dramatically. With digital recordings the loudest anything can be is 0 dBFS where the “FS” means Full Scale. This sets the maximum peak levels on the recording. Average volume is measured in dB below 0 dBFS and here’s a rough guide:

• Highly Compressed Pop (see pic above right): –6 dB to –9 dB
• Well Recorded Pop: –9 dB to –12 dB
• Well Recorded Acoustic/Jazz: –12 dB to –18 dB
• Wide Dynamic Range Classical: –18 dB to –30 dB

WHAT’S RMS? RMS is just a geeky way to, for the purposes of this discussion, describe the average level of a waveform. It’s roughly 1/3 the peak-to-peak value of a sine wave. For something as complex as music, the RMS value is much more complicated but still can be calculated by software analysis and measured by more sophisticated instruments.

WHY AVERAGE VOLUME MATTERS: If you include the extremes there’s a range of roughly 24 dB in average volume between different kinds of music. How much is 24 dB? If we take highly compressed pop recording and play it at given average volume a highly dynamic classical recording might require 250 times more peak power! This isn’t strictly a fair comparison as if you really tried to play the classic recording at that level you would likely be reaching for the volume control during the louder parts. But it illustrates how important the source material is in determining peak power requirements.

DIFFICULT MUSIC: The most challenging music is where the average volume is always relatively low prompting you to turn up the volume but there are very brief transients that are far higher in level. This is most common in audiophile recordings where very little or no compression is used and there are Sforzando (brief loud) notes in the music. This is very different than say symphonic classical music that builds up to fairly high sustained average levels  (i.e. crescendos) that will have you turning down the volume. Brief loud transients add impact to the music without making it seem much louder. Worst case, these brief transients can be 20+ dB above the average level requiring around 100 times more power than the average level. Compare the Flim and the BB’s – New America track in Audacity to the Lada Gaga – Just Dance track (the two screen shots above). Even during the “loud” part of New America the average level (light blue portion) is still relatively low.

CLIPPING: When the source doesn’t have enough voltage and/or current to meet the peak demands of the music it clips off the peaks. Studies have shown it may go unnoticed if it’s infrequent and mild. But if it happens often, or a single event is severe, it tends to be plainly audible as a harsh “grunge”. It’s the number one cause of plainly audible distortion in everything from cell phones to car stereos. In the waveform shown to the right the yellow trace is properly reproduced while the green trace is from a less capable amp and you can see what happens to the peaks in the music—they’re “clipped” off as if someone took scissors to the music.

DESIRED MAXIMUM VOLUME: So how loud is “loud enough”? To establish the upper end of subjective tastes, studies show the threshold of pain starts around 120 dB SPL. It seems reasonable to use that as the absolute upper limit. 120 dB SPL is also the level at which even short term exposure can cause permanent hearing impairment. Studies have shown even sustained average levels above 85 dB SPL can cause hearing damage. For more on these thresholds see Sound Pressure Levels. The research indicates the average maximum level should be at least 85 dB, and with classical music, that puts the peak level up to 30 dB higher at a worst case 115 dB). For more typical music peak levels of 110 dB SPL are more reasonable.

LIVE MUSIC: If you monitor sound pressure levels during live performances, rock concerts typically average 110 dB with peaks of 115 dB to 120 dB. Classical performances typically have peaks hitting 110 dB and a much lower average level of around 90 dB or less.

TESTING THE THEORY WITH POP MUSIC: I used my non-fatiguing HD650 headphones plugged into my O2 amplifier, and played several different selections of fairly well recorded pop music at levels as loud as I would ever want to listen—likely into hearing damage territory for any sort of sustained or cumulative listening. The HD650 needed about 1.7 – 1.8 Vrms which works about to about 107 dB SPL. The oscilloscope screenshot to the right (click for larger) shows the music and the the horizontal dashed lines are the peak-to-peak value (about 4.8V). Notice the marked peak isn’t all that far above the rest of the music. For this kind of music, and my subjective idea of what’s “too loud”, I’m close to the 110 dB SPL guideline established above. So far the guideline is holding up well.

TESTING WITH FLIM & THE BB’s: Next I repeated the above test but this time using the same Flim & the BB’s – New America track shown earlier. I set the volume to where the loudest parts of the track were about at my limit of still being “comfortable”. Now the peaks hit 5.1 volts in one direction or about 10.2 volt peak-to-peak (the sample in this case is about 9 V p-p). That’s about 3.2 – 3.6 Vrms which is about 114 dB from the HD650’s on the peaks. This at the limit of or beyond what most portable amps can manage (the O2 being a notable exception). This correlates well with the 115 dB rule of thumb for highly dynamic music. So, working backwards from the threshold of pain and hearing loss you get 105 – 115 dB. Using live performance levels you get 105 – 115 dB. And testing using my own music, ears, and headphones, I get 107 – 114 dB SPL. So, all things considered, 110 dB SPL seems like a good target if you want to pick just one number. Add 5 dB for really wide dynamic range music at live levels and subtract 5 dB if you listen to mostly Lady Gaga or don’t like it very loud.

HEADPHONE SENSITIVITY: Headphones need widely different amounts of power to play at the same loudness. How loud they get with a given amount of power is their Sensitivity or Efficiency. This number is properly specified as either dB SPL per milliwatt (1/1000 of a watt) or as dB SPL per volt. The older international standard used the milliwatt method and the newer method uses voltage. But sometimes manufactures don’t specify either in their specs—such as Ultrasone in the list below. The list shows a range of 87 dB to 117 dB at the same 1 mW of power. That’s 30 dB and, believe it or not, the HiFiMAN headphones need 1000 times more power to play at the same level as the TripleFi 10s!  Some examples:

• Sennheiser HD600: Sound pressure level (SPL) 97 dB (SPL) at 1 mW, 300 ohms
• Sennheiser HD650 - Sound pressure level (SPL) 103 dB (1 Vrms), 300 ohms
• Ultimate Ears TripleFi 10 - Sensitivity: 117 dB SPL/mW, 1 kHz, 32 ohms
• HiFiMAN HE-5LE - Sensitivity: 87.5 dB, 1 mW, 38 ohms
• Ultrasone Edition 10 – Sound Pressure Level 99 dB (useless spec!), 32 ohms

HEADPHONE IMPEDANCE: The impedance is listed at the end of the specs for each of the above headphones. It’s important to know the impedance if you want to convert between watts and volts—to say compare the HD600 to the HD650’s sensitivity. It’s also essential to estimate how much output a given source will have using a particular pair of headphones. Impedance is specified in ohms (Ω).

SOURCE MAXIMUM OUTPUT: This is where things often get vague. A lot of sources, including portable players, headphone DACs, and headphone amps, have incomplete output power specifications. The output power of any device is very dependent on the impedance of the headphones (known as the “load”). Power is a function of voltage and current. And, unfortunately, different sources have differing maximum amounts of both. Some, like Apple, keep it all a secret while others, like Sony, specify a useless value. The output impedance of the source (which is rarely specified) also alters the maximum power into different loads. So without complete specs it can be difficult to estimate. Here are some typical examples:

• Apple iPod Touch – Power not specified, output impedance not specified
• Sony NWZS545 – Audio Power Output: 5mW + 5mW (useless!), output impedance not specified
• NuForce uDAC-2 - Power output: 80mW x 2 @ 16-Ohm, output impedance not specified
• FiiO E7 – Output power: 150mW (16 Ohm); 16mW (300 Ohm), output impedance not specified
• FiiO E9 - Output power: 1W (16Ω); 80mW (600Ω), output impedance not specified
• Leckerton UHA-4 - 20mW 16 ohms, 40mW 32 ohms, 50mW 100 ohms, 15mW 300 ohms, output impedance 0.4 ohms

HEADROOM: The 105 – 115 dB guideline established above works fairly well without any extra headroom. But audio purists might want to add another 25% – 100% (1 – 3 dB) more power for a bit of extra headroom so the amp is even less likely to clip any peaks.

SUMMARY: The table at the start of this article can be used to get in the ball park and I’ve tried to explain how average volume and preferences also make a big difference. The more technically inclined may want to keep reading and learn how to calculate volume levels, convert between different specs, and more.

---

TECH SECTION (math ahead)

---

PERFECT SOURCES: As shown earlier, headphone and source specifications range from non-existent to fairly complete. Some headphone sources behave as a perfect voltage source. That means they will always produce the same output voltage no matter what reasonable load you connect. Even a headphone amp such as the $20 FiiO E5 can produce the same 1.2 Vrms into any load from 16 ohms (about as low as headphones go) to 600 ohms (the common upper limit). As long as you don’t need more than 1.2 V, it does a pretty good imitation of a perfect voltage source. This is because it has a low output impedance and enough current to drive 16 ohm loads without current limiting. With such a source the max power output is given by:

• P = (Vmax * Vmax) / Headphone Impedance

POWER EXAMPLES: For low impedance sources that have ample current available, such as the FiiO E5, here’s the same amp with 3 different headphones, note the widely different power outputs:

• HD600 (300 ohms) & FiiO E5 – (1.2 * 1.2)/300 = 4.8 mW
• Beyer DT770 (80 ohms) & FiiO E5 - (1.2 * 1.2)/80 = 18 mW
• TripleFi 10 (32 ohms) & FiiO E5 - (1.2 * 1.2)/32 = 45 mW

IMPERFECT SOURCES: In this case “imperfect” doesn’t necessarily mean bad, but several factors can limit the output of a given source. Any source can only manage so much voltage even with no load at all. It’s limited by the internal power supply voltage, and with most portable battery powered gear, is often relatively low. Most iPods can only manage about 0.5 – 1.0 Vrms maximum voltage, the FiiO E7 1.2 Vrms and the Leckerton UHA-4 about 2.2 Vrms into the highest impedance headphones (600 ohms). As the impedance drops, instead of the voltage staying the same, the voltage also may drop. This can be due to a significant output impedance and/or reaching the internal current limits (current limiting).

OUTPUT IMPEDANCE: Headphone sources have output impedances ranging from less than 1 ohm to 120 ohms or more. As the output impedance gets within about 1/8th of the headphone impedance it starts to significantly decrease the output available. The output impedance creates a voltage divider with the headphones.  It’s no longer close to being a perfect source as explained above. If an amp has a 50 ohm output impedance, and you plug in 50 ohm headphones, only one quarter as much power is delivered to the headphones compared with a zero ohm output impedance.

CURRENT LIMITING: Look at the specs for the Leckerton UHA-4 above. It puts out 50 mW at 100 ohms and that works out to 2.2 Vrms. If it could manage the same 2.2 Vrms into 16 ohms it should put out (2.2 * 2.2)/16 = 302 mW. but Leckerton only lists 20 mW. It has an output impedance of only 0.4 ohms so that’s not the problem. So what’s going on? The answer is some sources run out of current as the load impedance drops below some value. That’s what’s happening with the UHA-4. It just doesn’t have the beans to maintain the same voltage into loads much below 100 ohms. If a manufacture doesn’t specify the power output over a wide range of impedances it’s impossible to predict this behavior. Some might be tempted to argue that low impedance headphones are much more sensitive and need less power so this doesn’t matter, but that’s not always true. The HiFiMAN headphones above, many of the AKG models, and others, have low impedances and relatively low sensitivities. And they would be a poor match with something like the Leckerton.

CONNECTING THE DOTS: If a company doesn’t specify the power output around your headphone impedance you’re forced to try one of the following:

• Power Specified At A Lower Impedance – In this case you want to figure out the voltage at the lower impedance and use that instead. The math is V = SquareRoot( Power in Watts * Impedance ). So for the FiiO E7, for example, it’s SquareRoot ( 0.15 * 16 )  = 1.5 Vrms.
• Power Specified At A Higher Impedance – It’s impossible to accurately predict a source’s behavior into impedances lower than specified when you don’t know the output impedance or maximum current. The Leckerton UHA-4 example above shows how it goes wrong with current limiting. And the E9 shows how it goes wrong due to its higher (10 ohm) output impedance. The E9’s 80 mW into 600 ohms gives: SquareRoot ( 0.080 * 600 ) = 6.9 Vrms which should yield 3 watts at 16 ohms, but the E9 only manages 1 watt or 4 Vrms because a lot of power is lost due to the 10 ohm output impedance. A very rough estimate can be obtained by calculating the voltage at the next higher impedance, and then dividing that value by four to calculate power at lower impedances.
• To Many Unknowns – If you don’t know a device’s output into an impedance at least as low as your headphones, I would strongly suggesting choosing a different source with better specified output power (or voltage). Generally manufactures that don’t offer complete specs likely are trying to hide something or they many not even know themselves. Their potential customers should not be forced to guess if their gear will meet their needs. A better specified product is a much safer investment.

BRINGING IT ALL TOGETHER: If your eyes haven’t glazed over yet, it’s time to bring all of the above together. That involves converting between volts, power and decibels.

LOGARITHMS: Don’t panic, but the math involved requires a button that might not be on your calculator usually labeled “LOG” (base 10 logarithms are known as LOG10 in spreadsheets) and the inverse usually labeled “10^x” (base 10 antilog or POWER(10,value) in spreadsheets). There are some online logarithm calculators that can also help with the math.

CALCULATE SPL FROM POWER: If you have a given source, and want to know how loud your headphones will get, you need to know the sensitivity of your headphones in dB/mW and the output power of the source in mW at the headphone impedance. Here’s the equation and the the FiiO E5 driving the HD600s (from above):

• dBSPL = Sensitivity in dB/mW + 10 * LOG ( Pmax in mW)
• 97 + 10 * LOG ( 5.6 ) = 103.8 peak dB SPL for HD600 & FiiO E5

CALCULATE SPL FROM VOLTAGE: If you know the voltage of your source at your headphone impedance, and your headphones sensitivity is rated at 1 volt, you can calculate the maximum output using the FiiO E5 and the HD650:

• dB SPL = Sensitivity in dB/volt + 20 * LOG ( Vmax)
• 103 + 20 * LOG ( 1.2 ) = 104.6 peak dB SPL for HD650 & FiiO E5

HOW LOUD WILL IT BE? The rule of thumb established above is 110 dB SPL for peak levels with a reasonable range of 105 – 115 dB depending on music and preferences. The E5 obviously falls a bit short with either the HD600 or the HD650 but it might still get loud enough for some tastes—especially with heavily compressed pop music with a high average volume. So let’s work the numbers the other way and see how much power the same headphones ideally need.

CALCULATE POWER FROM SPL: Using the HD600, rated in dB/mW you get:

• Power in mW = Antilog ( ( Desired SPL - SPL at 1 mW ) / 10 )
• Antilog ( ( 110 - 97 ) / 10 ) = 20 mW for HD600 to hit 110 dB SPL peak
• Antilog ( ( 115 - 97 ) / 10 ) = 63 mW for HD600 to hit 115 dB SPL peak

CALCULATE VOLTAGE FROM SPL: As above except for the HD650 rates in volts we get:

• Voltage RMS = Antilog ( ( Desired SPL – SPL at 1Vrms) /20 )
• Antilog ( ( 110 – 103) / 20 ) = 2.2 Vrms for HD650 to hit 110 dB SPL peak
• Antilog ( ( 115 – 103) / 20 ) = 4.0 Vrms for HD650 to hit 115 dB SPL peak

TO CONVERT FROM OTHER SPECS: Sometimes you might find things specified a bit differently. InnerFidelity, for example, measures headphones at the voltage required for 90 dB SPL. Here are some conversions:

• 90 dB Voltage to SPL at 1 Volt: SPL at 1 Volt = 90 + 20 * LOG ( 1 / V_90db )
• Voltage to Power : Power in Watts = ( V * V ) / Impedance
• Power to Voltage: Voltage = SquareRoot ( Power * Impedance )
• Decibels from Two Voltages: dB = 20 * LOG ( V1 / V2 )
• Decibels from Two Powers: dB = 10 * LOG ( P1 / P2 )
• Volts p-p To Volts RMS: Vrms = Vp-p * 0.354
• Vrms to Vp-p: Vp-p = Vrms * 2.83

DOING IT RIGHT: The best manufactures specify a device’s power output at several impedances—including the extremes of 16 and 600 ohms. The Leckerton example earlier is one example and another is Violectric’s Specification Page. The best measurements do the same thing. Here, for example, is the output of the O2 amplifier vs THD into several loads. You can see the distortion remains very low until the amp reaches clipping and then the distortion quickly goes nearly vertical and off the top of the graph. The 1% THD point is the generally accepted level for maximum output. The O2 has current limiting to help avoid damaging low impedance headphones. That’s why the 15 ohm and 33 ohm output voltages are lower. But you’ll notice at 80, 150 and 600 ohms the voltages are almost identical at about 7.3 Vrms because the output impedance is very low and the O2 is behaving essentially as a perfect voltage source:

MEASURING MAXIMUM OUTPUT: To measure output power correctly specialized equipment is required. RMAA has no concept of absolute levels (such as voltage) and it can’t plot output vs THD as seen above so it’s not very helpful. It’s also easy to damage a soundcard’s input which typically have a maximum input of 2 Vrms or less. You can make a very crude measurement using an oscilloscope with a known load resistance (don’t use headphones) and increasing the level until barely visible clipping is observed. Ideally the test is done with a 60 hz sine wave and a DMM used to read the RMS voltage (most DMMs are only accurate around 60 hz and not at higher frequencies). You can also read the peak-to-peak voltage from the scope but that’s less accurate. Tests should be brief (only a few seconds at full power) into lower impedance loads as sustained sine wave testing can exceed the thermal limits of many devices. Without a scope or distortion/audio analyzer it’s very difficult to get accurate output measurements.

BOTTOM LINE: Hopefully, especially for the more technically (or at least mathematically) inclined, this article sheds a bit more light on power output and volume levels. Once you get past the math, the main hurdle is incomplete specifications. The best remedy for shoddy specs is to simply spend your money on products from companies that are not afraid to publish detailed specs. The others will eventually get the message.

OTHER RESOURCES: These may also be useful:

• Headphone Amps Explained
• All About Gain 
• Noise And Dynamic Range